CS50Lecture5

这仅仅是我个人的学习笔记，没有什么干货，可能会有写错的信息，不推荐观看学习!

Data Structures

• Data structures essentially are forms of organization in memory.
• There are many ways to organize data in memory
• Abstract data structures are those that we can conceptually imagine. When learning about computer science, it’s often useful to begin with these conceptual data structures. Learning these will make it easier later to understand how to implement more concrete data structures.

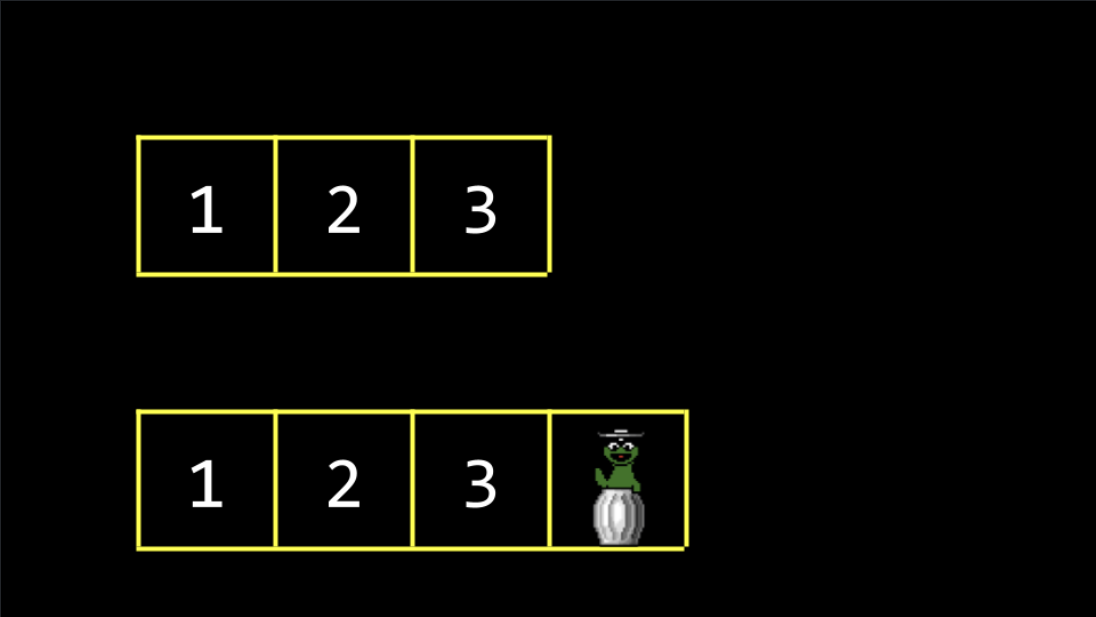
Stacks and Queues

• Queues are one form of abstract data structure.
• Queues have specific properties. Namely, they are FIFO or “first in first out.” You can imagine yourself in a line for a ride at an amusement park. The first person in the line gets to go on the ride first. The last person gets to go on the ride last.
• Queues have specific actions associated with them. For example, an item can be enqueued; that is, the item can join the line or queue. Further, an item can be dequeued or leave the queue once it reaches the front of the line.
• Euqueue 是指将一个元素添加到队列的末尾。dequeue 是指从队列的前面移除一个元素
• Queues 与 Stack 形成鲜明对比。从根本上说，Stack 的属性与 Queue 不同，Stack 是 LIFO 也就是 “last in first out”。就像自助餐厅里的托盘堆叠一样，最后放入堆叠中的托盘可能最先被取走，Jack Learns the Facts About Queues and Stacks
• Stacks have specific actions associated with them. For example, push places something on top of a stack. Pop is removing something from the top of the stack.
• In code, you might imagine a stack as follows:

typedef struct
{
    person people[CAPACITY];
    int size;
}
stack;

Notice that an array called people is of type person. The CAPACITY is how high the stack could be. The integer size is how full the stack actually is, regardless of how much it could hold.

• You might imagine that the above code has a limitation. Since the capacity of the array is always predetermined in this code. Therefore, the stack may always be oversized. You might imagine only using one place in the stack out of 5000.
• It would be nice for our stack to be dynamic – able to grow as items are added to it.

Resizing Arrays

• An array is a block of contiguous memory.

• You might imagine an array as follows:

• In memory, there are other values being stored by other programs, functions, and variables. Many of these may be unused garbage values that were utilized at one point but are available now for use.

• Imagine you wanted to store a fourth value 4 in our array? What would be needed is to allocate a new area of memory and move the old array to a new one. Initially, this new area of memory would be populated with garbage values.

• As values are added to this new area of memory, old garbage values would be overwritten.

• Eventually, all old garbage values would be overwritten with our new data.

• One of the drawbacks of this approach is that it’s bad design: Every time we add a number, we have to copy the array item by item.

• 如果我们能把4放在内存的其他地方，岂不更好？根据定义，这将不再是一个数组，因为4不再位于连续的内存中。

// Implements a list of numbers with an array of fixed size

#include <stdio.h>

int main(void)
{
    // List of size 3
    int list[3];

    // Initialize list with numbers
    list[0] = 1;
    list[1] = 2;
    list[2] = 3;

    // Print list
    for (int i = 0; i < 3; i++)
    {
        printf("%i\n", list[i]);
    }
}

• We have memory being preallocated for three items.
• Building upon our knowledge obtained more recently, we can leverage our understanding of pointers to create a better design in this code. Modify your code as follows:

// Implements a list of numbers with an array of dynamic size

#include <stdio.h>
#include <stdlib.h>

int main(void)
{
    // List of size 3
    int *list = malloc(3 * sizeof(int));
    if (list == NULL)
    {
        return 1;
    }

    // Initialize list of size 3 with numbers
    list[0] = 1;
    list[1] = 2;
    list[2] = 3;

    // List of size 4
    int *tmp = malloc(4 * sizeof(int));
    if (tmp == NULL)
    {
        free(list);
        return 1;
    }

    // Copy list of size 3 into list of size 4
    for (int i = 0; i < 3; i++)
    {
        tmp[i] = list[i];
    }

    // Add number to list of size 4
    tmp[3] = 4;

    // Free list of size 3
    free(list);

    // Remember list of size 4
    list = tmp;

    // Print list
    for (int i = 0; i < 4; i++)
    {
        printf("%i\n", list[i]);
    }

    // Free list
    free(list);
    return 0;
}

Notice that a list of size three integers is created. Then, three memory addresses can be assigned the values 1, 2, and 3. Then, a list of size four is created. Next, the list is copied from the first to the second. The value for the 4 is added to the tmp list. Since the block of memory that list points to is no longer used, it is freed using the command free(list). Finally, the compiler is told to point list pointer now to the block of memory that tmp points to. The contents of list are printed and then freed.

• It’s useful to think about list and tmp as both signs that point at a chunk of memory. As in the example above, list at one point pointed to an array of size 3. By the end, list was told to point to a chunk of memory of size 4. Technically, by the end of the above code, tmp and list both pointed to the same block of memory.

Linked List

• c A struct is a data type that you can define yourself. A . in dot notation allows you to access variables inside that structure. The * operator is used to declare a pointer or dereference a variable.

• Today, you are introduced to the -> operator. It is an arrow. This operator goes to an address and looks inside of a structure.

• A linked list is one of the most powerful data structures within C. A linked list allows you to include values that are located at varying areas of memory. Further, they allow you to dynamically grow and shrink the list as you desire.

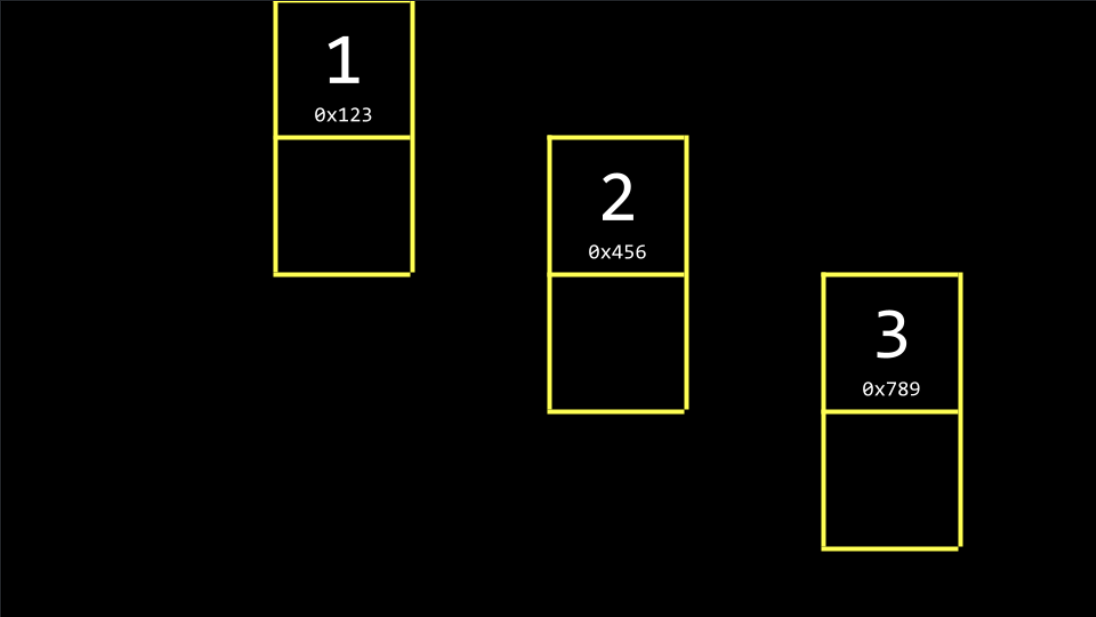
• You might imagine three values stored at three different areas of memory as follows:

• We could imagine this data pictured above as follows:

• We could utilize more memory to keep track of where the next item is. 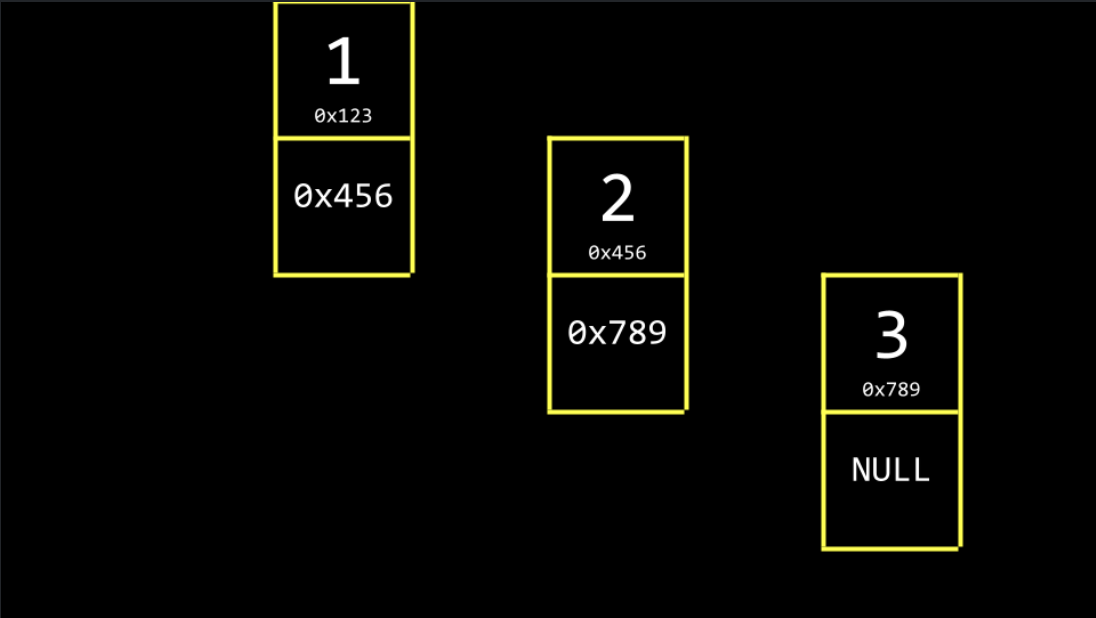Notice that NULL is utilized to indicate that nothing else is next in the list.

• By convention, we would keep one more element in memory, a pointer, that keeps track of the first item in the list.

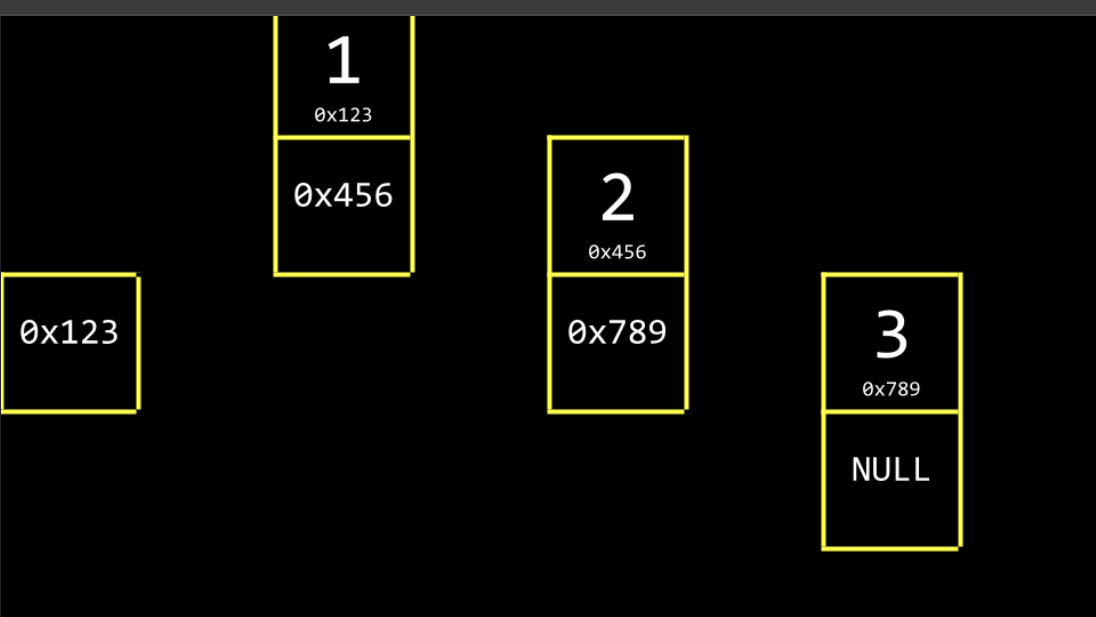
• Abstracting away the memory addresses, the list would appear as follows:

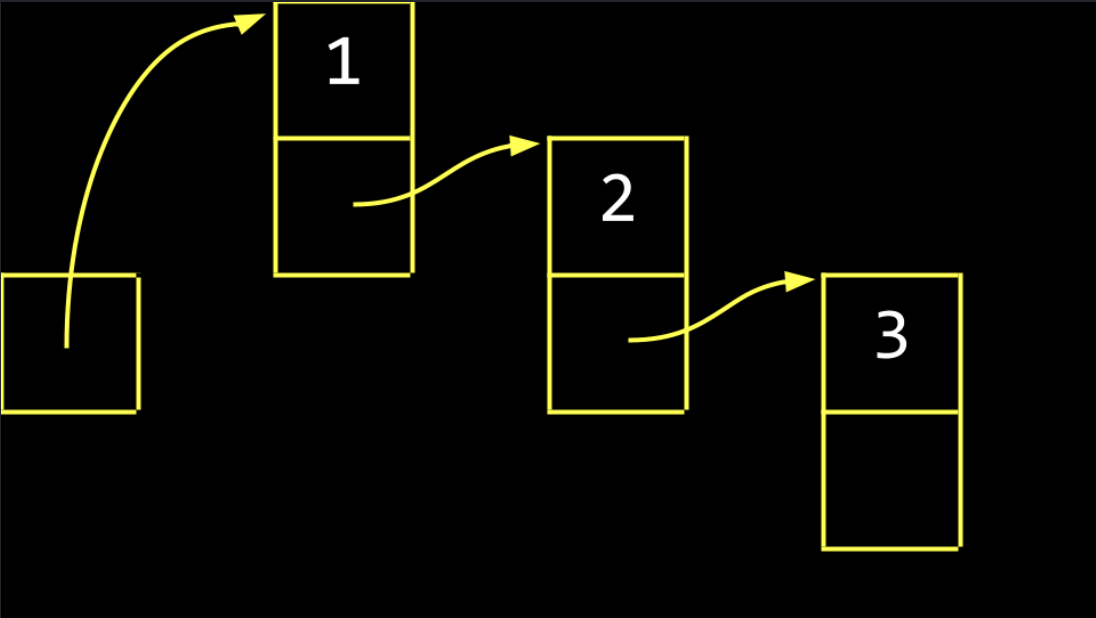
• These boxes are called nodes. A node contains both an item and a pointer called next. In code, you can imagine a node as follows:

typedef struct node
{
    int number;
    struct node *next;
}
node;

Notice that the item contained within this node is an integer called number. Second, a pointer to a node called next is included, which will point to another node somewhere in memory.

• Conceptually, we can imagine the process of creating a linked list. First, node *list is declared, but it is of a garbage value.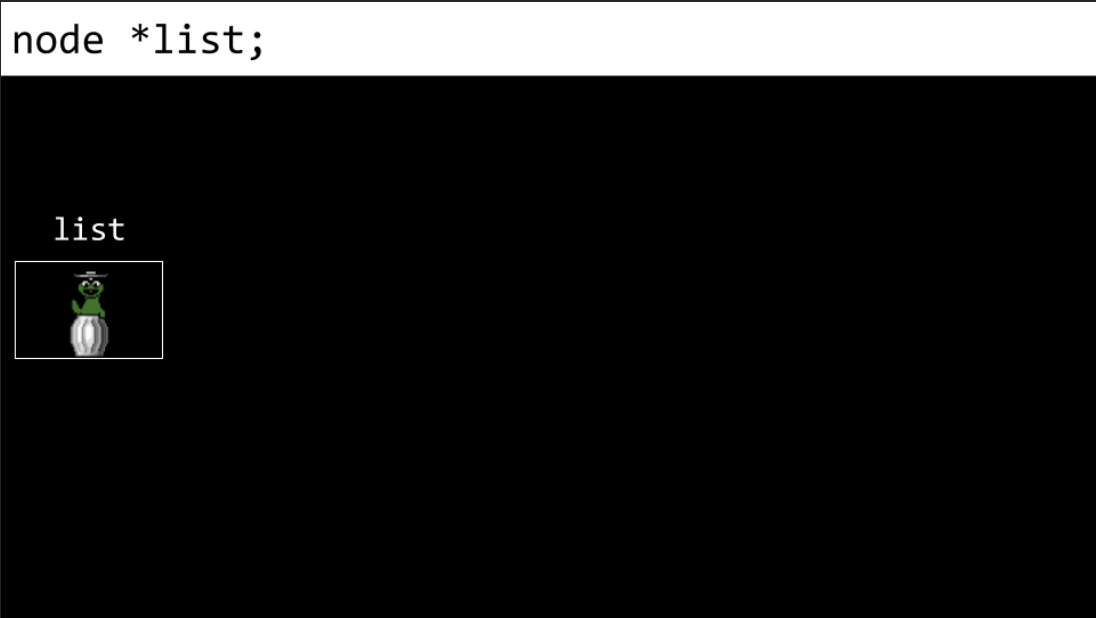

• Next, a node called n is allocated in memory.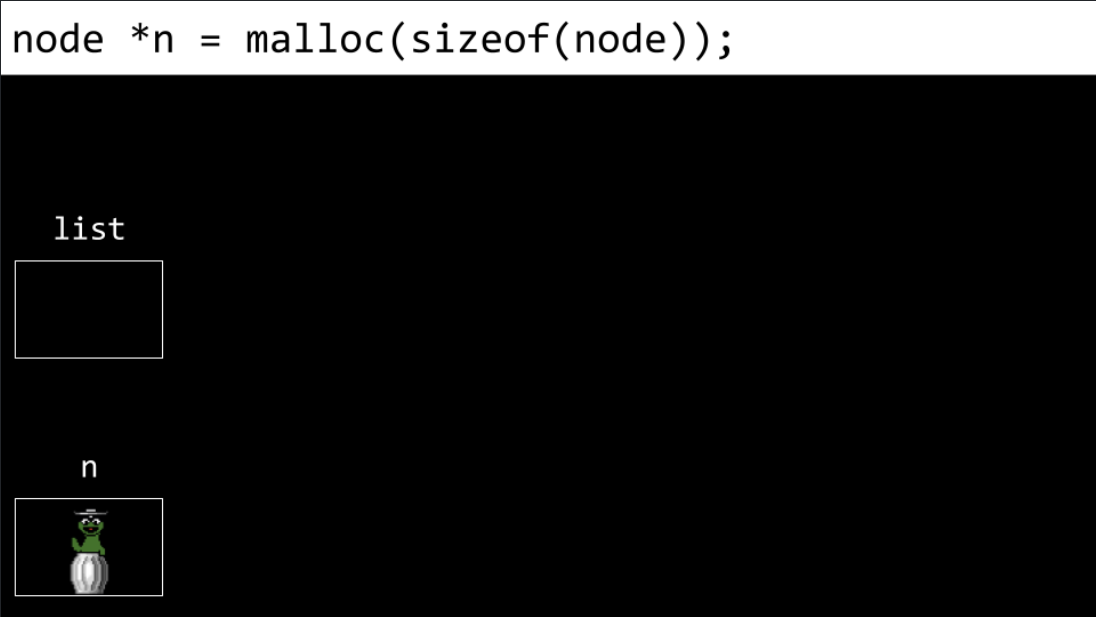

• Next, the number of node is assigned the value 1.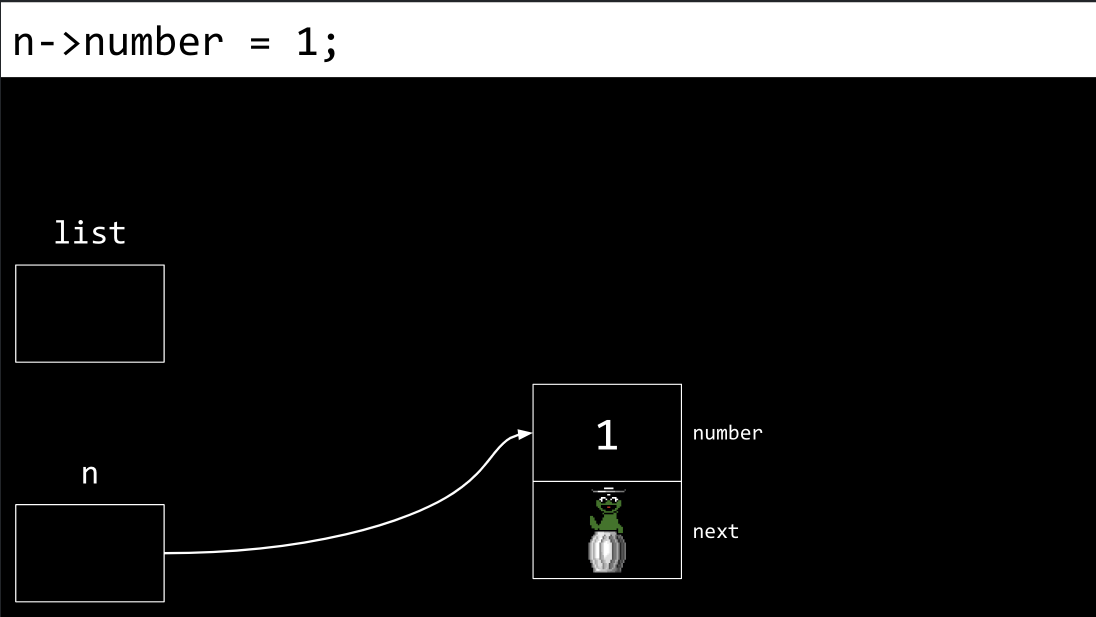

• Next, the node’s next field is assigned NULL.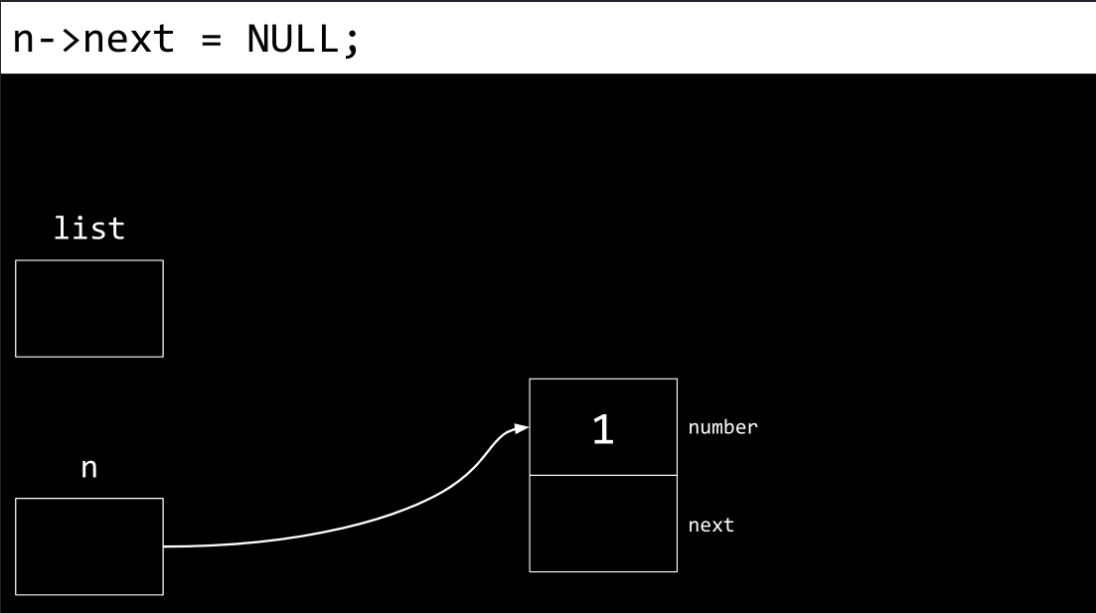

• Next, list is pointed at the memory location to where n points. n and list now point to the same place.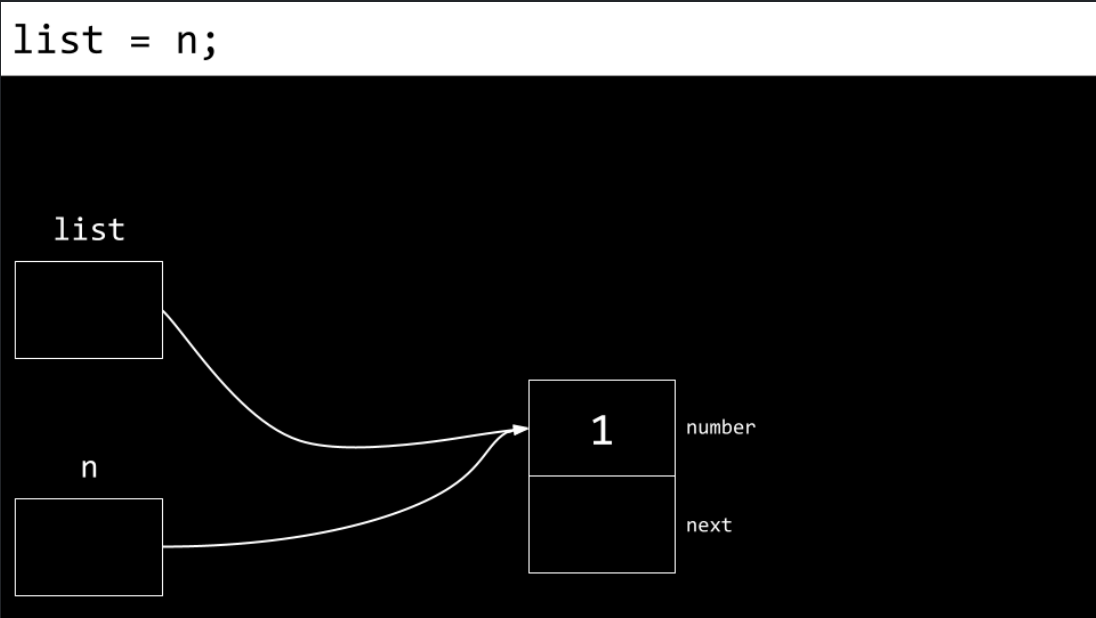

• A new node is then created. Both the number and next field are both filled with garbage values.。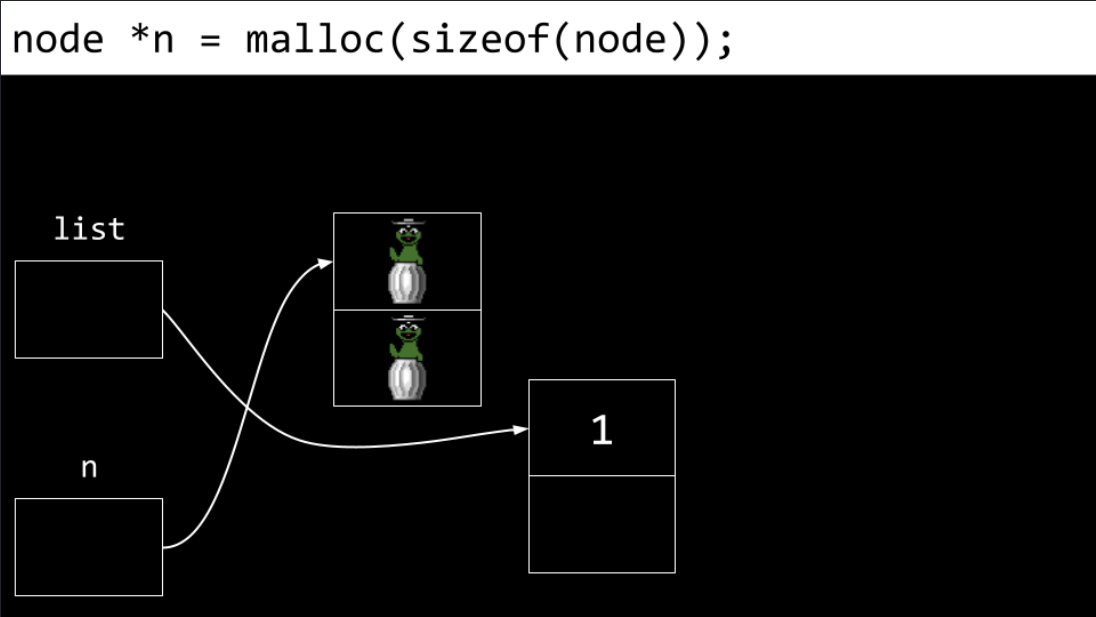

• The number value of n’s node (the new node) is updated to 2.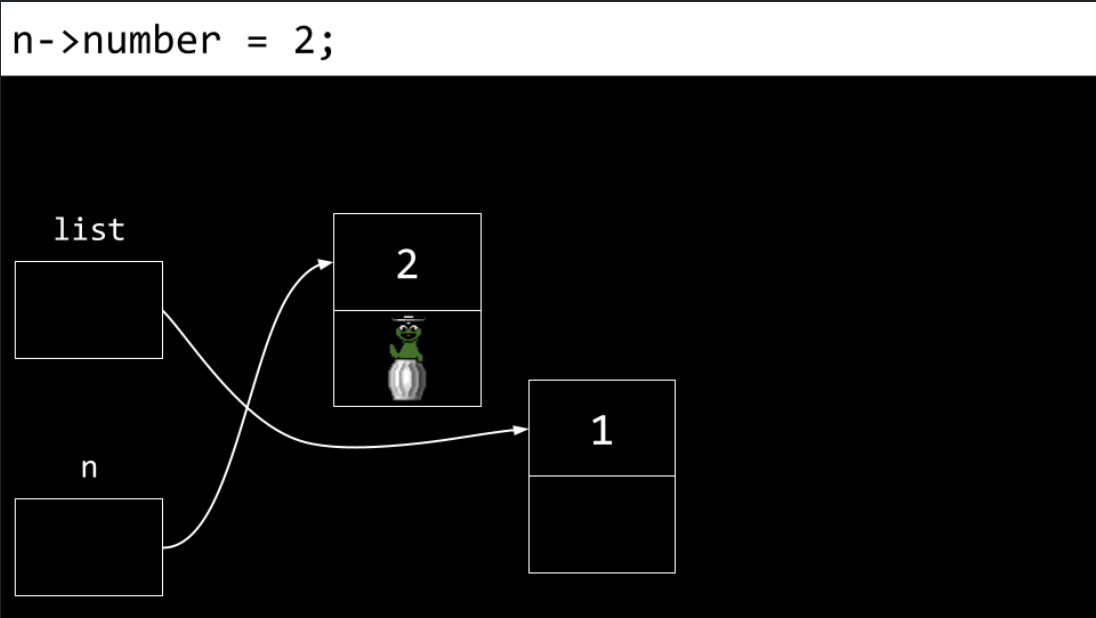

• Also, the next field is updated as well.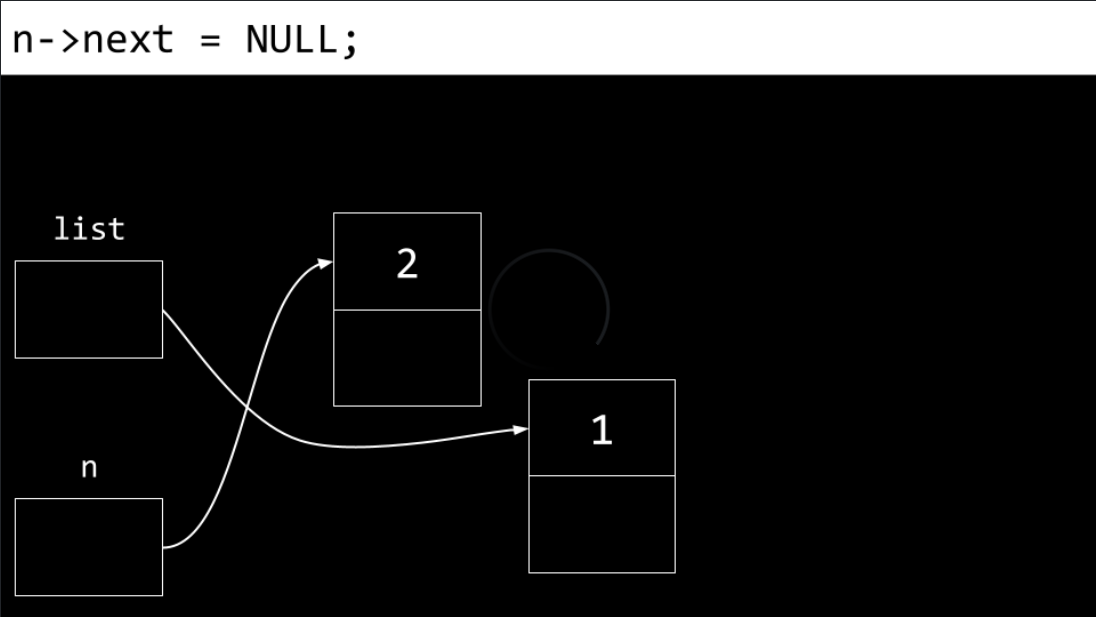

• Most important, we do not want to lose our connection to any of these nodes lest they be lost forever. Accordingly, n’s next field is pointed to the same memory location as list.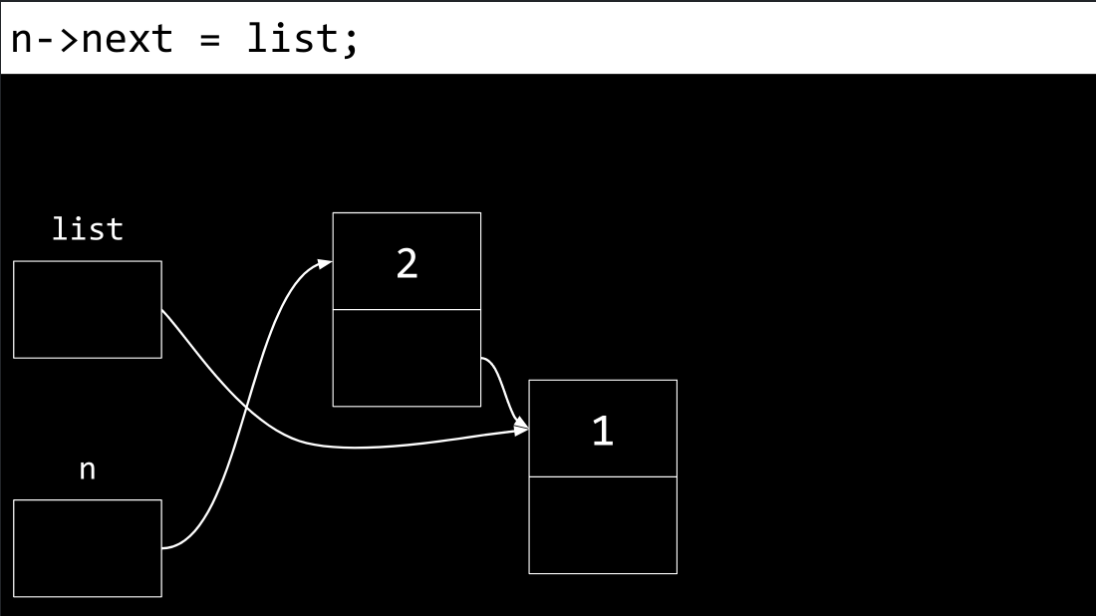

• Finally, list is updated to point at n. We now have a linked list of two items.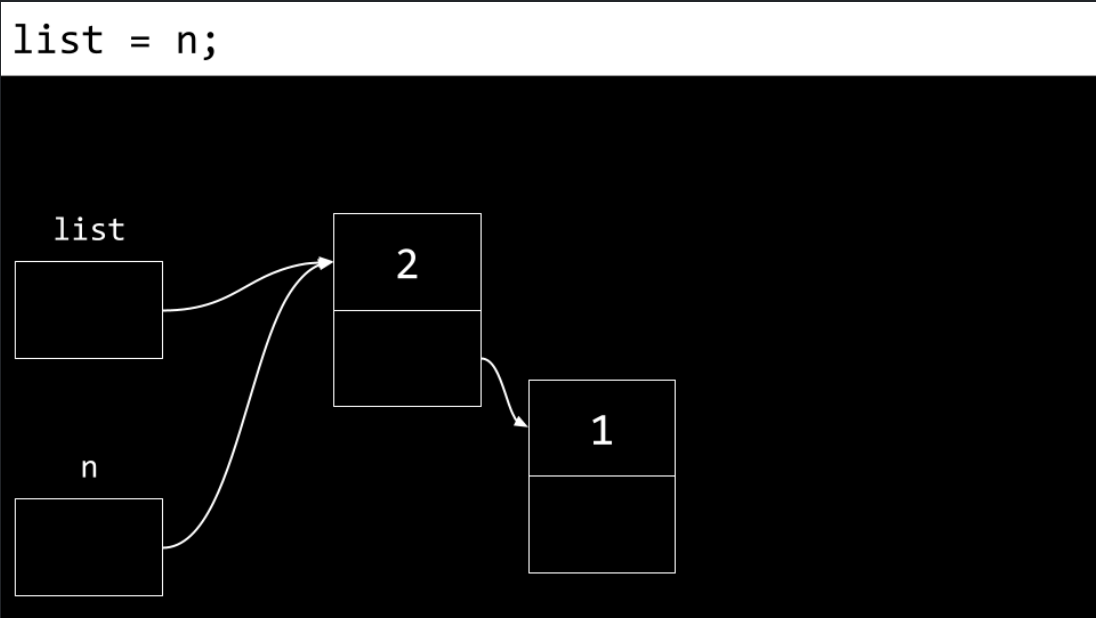

• To implement this in code, modify your code as follows:

// Prepends numbers to a linked list, using while loop to print

#include <cs50.h>
#include <stdio.h>
#include <stdlib.h>

typedef struct node
{
    int number;
    struct node *next;
}
node;

int main(int argc, char *argv[])
{
	// argc "argument count 命令行参数的数量"
	// argv "argument vector 一个字符串数组，存储命令行参数的实际值"
    // Memory for numbers
    node *list = NULL;

    // For each command-line argument
    for (int i = 1; i < argc; i++)
    {
        // Convert argument to int
        int number = atoi(argv[i]); //ASCII to integer

        // Allocate node for number
        node *n = malloc(sizeof(node));
        if (n == NULL)
        {
            return 1;
        }
        n->number = number;
        n->next = NULL;

        // Prepend node to list
        n->next = list;
        list = n;
    }

    // Print numbers
    node *ptr = list;
    while (ptr != NULL)
    {
        printf("%i\n", ptr->number);
        ptr = ptr->next;
    }

    // Free memory
    ptr = list;
    while (ptr != NULL)
    {
        node *next = ptr->next;
        free(ptr);
        ptr = next;
    }
}

注意，用户在命令行输入的内容被放入一个名为 number 的节点 n 的字段中，然后该节点被添加到 list 中。例如，./list 1 2 将数字 1 放入一个名为 number 的节点 n 的字段中，然后将指向 list 的指针放入该节点的 next 字段中，接着更新 list 以指向 n。对于 2，同样的过程会重复进行。接下来，node *ptr = list 创建一个临时变量，指向与 list 相同的位置。while 打印 ptr 指向的节点内容，然后更新 ptr 以指向列表中的 next 节点。最后，释放所有内存

在这个例子中，插入到列表中的顺序始终是 O(1) ，因为在列表前面插入只需要非常少的步骤。

考虑到搜索此列表所需的时间，它的复杂度为 O(n) ，因为在最坏的情况下，必须始终搜索整个列表才能找到一个项目。向列表中添加新元素的时间复杂度将取决于该元素添加的位置。以下示例对此进行了说明。

链表并不是存储在连续的内存块中。只要有足够的系统资源，它们可以无限增长。然而，缺点是需要更多的内存来跟踪列表，而不是数组。这是因为对于每个元素，您不仅必须存储元素的值，还必须存储指向下一个节点的指针。此外，链表不能像数组那样进行索引，因为我们需要遍历前 n−1 个元素才能找到第 n 个元素的位置。因此，上面所示的列表必须进行线性搜索。因此，在上述构造的列表中，二分搜索是不可能的。

• 进一步地，您可以在列表末尾放置数字，如以下代码所示

// Implements a sorted list of numbers using a linked list

#include <cs50.h>
#include <stdio.h>
#include <stdlib.h>

typedef struct node
{
    int number;
    struct node *next;
}
node;

int main(int argc, char *argv[])
{
    // Memory for numbers
    node *list = NULL;

    // For each command-line argument
    for (int i = 1; i < argc; i++)
    {
        // Convert argument to int
        int number = atoi(argv[i]);

        // Allocate node for number
        node *n = malloc(sizeof(node));
        if (n == NULL)
        {
            return 1;
        }
        n->number = number;
        n->next = NULL;

        // If list is empty
        if (list == NULL)
        {
            list = n;
        }

        // If number belongs at beginning of list
        else if (n->number < list->number)
        {
            n->next = list;
            list = n; 
        }

        // If number belongs later in list
        else
        {
            // Iterate over nodes in list
            for (node *ptr = list; ptr != NULL; ptr = ptr->next)
            {
                // If at end of list
                if (ptr->next == NULL)
                {
                    // Append node
                    ptr->next = n;
                    break;
                }

                // If in middle of list
                if (n->number < ptr->next->number)
                {
                    n->next = ptr->next;
                    ptr->next = n;
                    break;
                }
            }
        }
    }

    // Print numbers
    for (node *ptr = list; ptr != NULL; ptr = ptr->next)
    {
        printf("%i\n", ptr->number);
    }

    // Free memory
    node *ptr = list;
    while (ptr != NULL)
    {
        node *next = ptr->next;
        free(ptr);
        ptr = next;
    }
}

注意这个列表在构建时是如何排序的。为了以这种特定顺序插入一个元素，我们的代码在每次插入时仍然会运行在 O(n) ，因为在最坏的情况下，我们必须查看所有当前元素。

Trees

• Binary search trees are another data structure that can be used to store data more efficiently such that it can be searched and retrieved.

• You can imagine a sorted sequence of numbers.

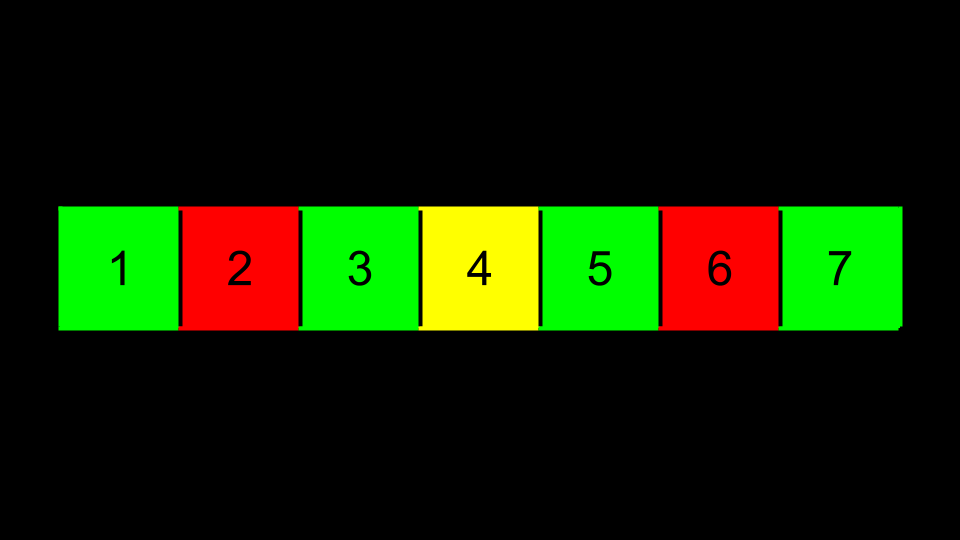
• Imagine then that the center value becomes the top of a tree. Those that are less than this value are placed to the left. Those values that are more than this value are to the right.

• Pointers can then be used to point to the correct location of each area of memory such that each of these nodes can be connected.

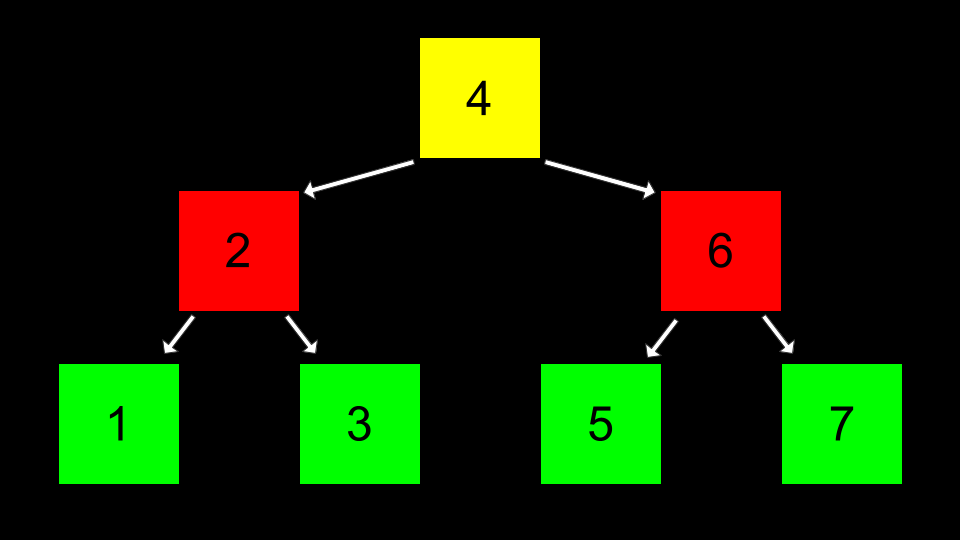
• In code, this can be implemented as follows.

// Implements a list of numbers as a binary search tree

#include <stdio.h>
#include <stdlib.h>

// Represents a node
typedef struct node
{
    int number;
    struct node *left;
    struct node *right;
}
node;

void free_tree(node *root);
void print_tree(node *root);

int main(void)
{
    // Tree of size 0
    node *tree = NULL;

    // Add number to list
    node *n = malloc(sizeof(node));
    if (n == NULL)
    {
        return 1;
    }
    n->number = 2;
    n->left = NULL;
    n->right = NULL;
    tree = n;

    // Add number to list
    n = malloc(sizeof(node));
    if (n == NULL)
    {
        free_tree(tree);
        return 1;
    }
    n->number = 1;
    n->left = NULL;
    n->right = NULL;
    tree->left = n;

    // Add number to list
    n = malloc(sizeof(node));
    if (n == NULL)
    {
        free_tree(tree);
        return 1;
    }
    n->number = 3;
    n->left = NULL;
    n->right = NULL;
    tree->right = n;

    // Print tree
    print_tree(tree);

    // Free tree
    free_tree(tree);
    return 0;
}

void free_tree(node *root)
{
    if (root == NULL)
    {
        return;
    }
    free_tree(root->left);
    free_tree(root->right);
    free(root);
}

void print_tree(node *root)
{
    if (root == NULL)
    {
        return;
    }
    print_tree(root->left);
    printf("%i\n", root->number);
    print_tree(root->right);
}

Notice this search function begins by going to the location of tree. Then, it uses recursion to search for number. The free_tree function recursively frees the tree. print_tree recursively prints the tree.

• A tree like the above offers dynamism that an array does not offer. It can grow and shrink as we wish.
• Further, this structure offers a search time of O(logn).

Dictionaries

• Dictionaries are another data structure.
• Dictionaries, like actual book-form dictionaries that have a word and a definition, have a key and a value.
• The holy grail of algorithmic time complexity is O(1) or constant time. That is, the ultimate is for access to be instantaneous.
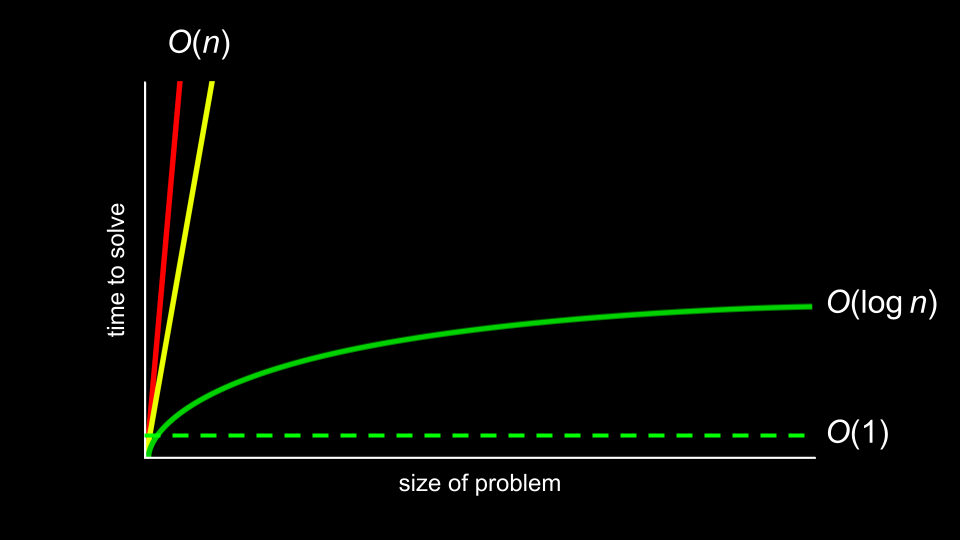
• • Dictionaries can offer this speed of access through hashing.

Hashing and Hash Tables

• Hashing is the idea of taking a value and being able to output a value that becomes a shortcut to it later.

• For example, hashing apple may hash as a value of 1, and berry may be hashed as 2. Therefore, finding apple is as easy as asking the hash algorithm where apple is stored. While not ideal in terms of design, ultimately, putting all a’s in one bucket and b’s in another, this concept of bucketizing hashed values illustrates how you can use this concept: a hashed value can be used to shortcut finding such a value.

• A hash function is an algorithm that reduces a larger value to something small and predictable. Generally, this function takes in an item you wish to add to your hash table, and returns an integer representing the array index in which the item should be placed.

• A hash table is a fantastic combination of both arrays and linked lists. When implemented in code, a hash table is an array of pointers to _node_s.

• A hash table could be imagined as follows: Notice that this is an array that is assigned each value of the alphabet.

• Then, at each location of the array, a linked list is used to track each value being stored there:

• Collisions are when you add values to the hash table, and something already exists at the hashed location. In the above, collisions are simply appended to the end of the list.

• Collisions can be reduced by better programming your hash table and hash algorithm. You can imagine an improvement upon the above as follows:

• Consider the following example of a hash algorithm:

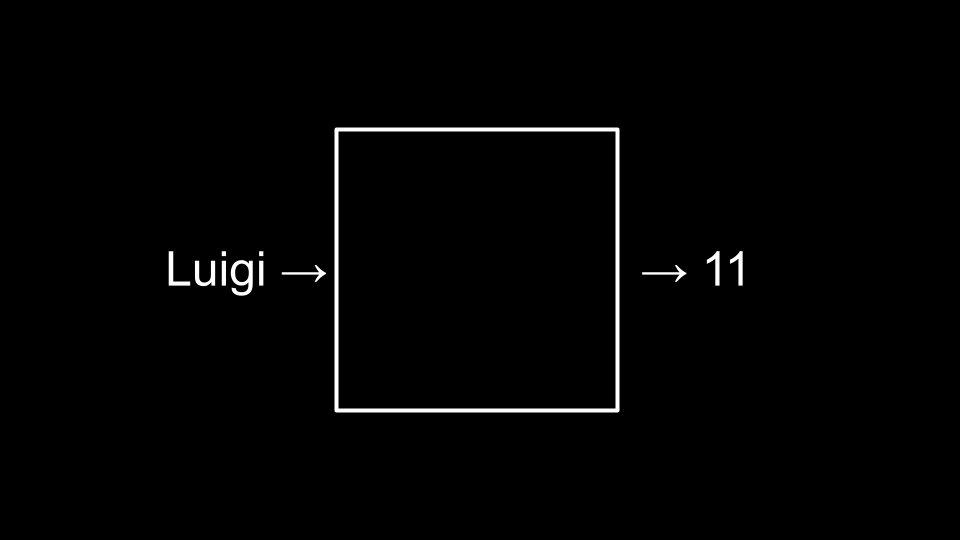
• This could be implemented in code as:

#include <ctype.h>

unsigned int hash(const char *word)
{
    return toupper(word[0]) - 'A';
}

Notice how the hash function returns the value of toupper(word[0]) - 'A'.

• You, as the programmer, have to make a decision about the advantages of using more memory to have a large hash table and potentially reducing search time or using less memory and potentially increasing search time.

Tries

• Tries are another form of data structure.

• Tries are always searchable in constant time.

• One downside to Tries is that they tend to take up a large amount of memory. Notice that we need 26×4=104 nodes just to store Toad!

• Toad would be stored as follows:

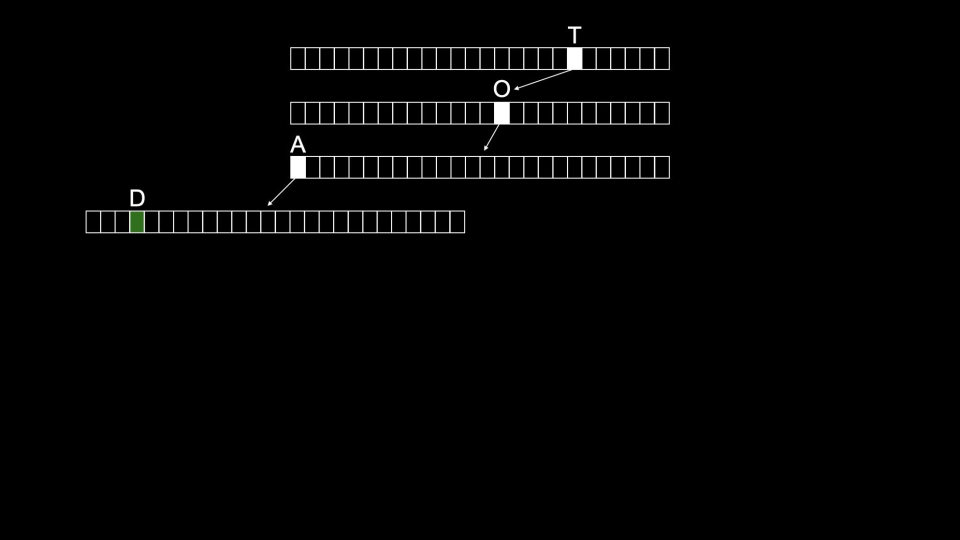
• Tom would then be stored as follows:

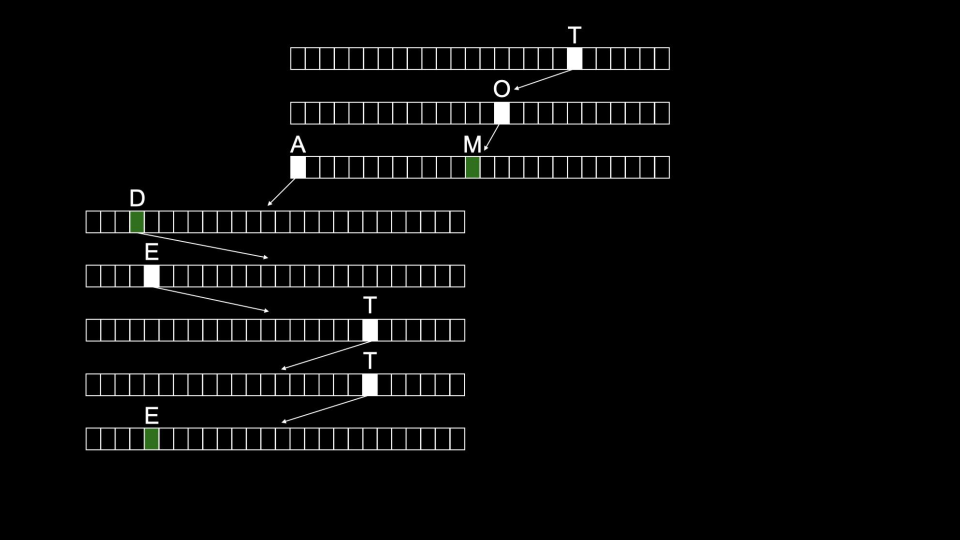
• The downside of this structure is how many resources are required to use it.